In the grand structure of mathematics, Abstract Algebra is often viewed as one of its most intellectually rigorous yet profoundly powerful pillars. While more elementary topics like linear algebra or calculus provide tools for solving numerical or geometric problems, abstract algebra ventures into the foundations of structure itself. It examines systems such as groups, rings, fields, and modules, abstracting and generalising familiar arithmetic rules to explore patterns that underpin much of modern mathematics and computer science.
What Is Abstract Algebra?
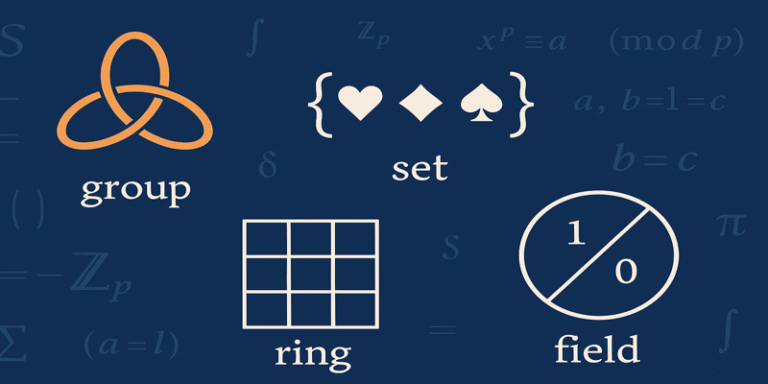
Abstract Algebra, sometimes called modern algebra, is the study of algebraic structures—sets equipped with operations that follow specific rules. Unlike elementary algebra, which deals with solving equations like x2+5x+6=0x^2 + 5x + 6 = 0x2+5x+6=0, abstract algebra is concerned with the logical consistency and internal symmetries of structures. According to Fraleigh (2013), the aim is not just to solve equations but to understand what kinds of equations are possible and why certain algebraic systems behave the way they do.
Among the most important structures in abstract algebra are:
- Groups: A group is a set with a single binary operation that satisfies four conditions—closure, associativity, identity, and invertibility. Groups are used to model symmetries in mathematics, art, and nature.
- Rings: A ring includes two operations, typically addition and multiplication, and generalises familiar structures like the integers.
- Fields: Fields are rings in which every non-zero element has a multiplicative inverse, such as the set of rational numbers or real numbers.
Each of these structures encapsulates core mathematical ideas in a way that is axiomatic, allowing mathematicians to generalise and apply them across a vast range of problems.
Historical Development
The roots of abstract algebra date back to the solutions of polynomial equations in the 16th and 17th centuries. However, the formalisation of the subject began in the 19th century with mathematicians like Évariste Galois, who introduced group theory to understand the solvability of equations. His revolutionary work showed that not all equations can be solved using radicals, and his ideas became foundational in developing group theory (Stewart, 2004).
Later, figures like Emmy Noether extended the theory of rings and ideals, making abstract algebra an indispensable language in many branches of mathematics, including topology, number theory, and algebraic geometry.
Educational and Cognitive Perspectives
Abstract algebra is notoriously difficult for students, not because of computational complexity, but due to its level of abstraction. Students are often expected to work with unfamiliar symbols, construct formal proofs, and generalise across multiple systems with little reliance on visual aids or concrete examples.
As Mohanty (2024) notes, the study of abstract algebra “poses significant cognitive challenges, requiring a shift from procedural to conceptual understanding.” To aid in comprehension, educators now often employ conceptual scaffolding—a method that introduces complex ideas gradually while reinforcing foundational concepts. This approach has shown promise in helping students internalise algebraic structures and appreciate their underlying logic (Mohanty, 2024).
Applications Beyond Mathematics
Though abstract algebra is inherently theoretical, it has remarkable applications in a variety of disciplines.
1.0 Cryptography
Modern digital security depends heavily on group theory and finite fields. The RSA encryption algorithm, for example, is built on the principles of modular arithmetic and Euler’s theorem, both of which are deeply rooted in algebraic concepts (Stinson & Paterson, 2018). Cryptographic protocols like elliptic curve cryptography use the algebraic structure of elliptic curves over finite fields, providing robust security with relatively small key sizes.
2.0 Coding Theory
Abstract algebra plays a central role in error-correcting codes, which are essential for reliable data transmission over noisy channels. Structures like finite fields and vector spaces over GF(2) (the field with two elements) form the mathematical foundation of Reed–Solomon codes, used in applications ranging from CDs and DVDs to QR codes and satellite communications (Huffman & Pless, 2010).
3.0 Quantum Computing
In quantum computation, algebraic structures are used to represent quantum gates, states, and operations. Group theory, in particular, helps describe the symmetries of quantum systems, while algebraic topology and module theory are increasingly used to model topological quantum computation—a field that aims to build fault-tolerant quantum machines (Nielsen & Chuang, 2010).
4.0 Chemistry and Physics
In molecular chemistry, the symmetry groups of molecules are studied using group theory to understand molecular vibrations and spectroscopic transitions. In physics, Lie groups and Lie algebras are used to model continuous symmetries in relativity and quantum field theory (Hall, 2015).
The Power of Abstraction
What makes abstract algebra so compelling is its generality. A single theorem proven for a group, for instance, can instantly apply to a wide variety of mathematical and real-world systems—be it the integers under addition, the rotations of a polygon, or the permutations of a Rubik’s Cube. This level of unification and elegance is what makes abstract algebra not just a toolkit but a philosophical framework.
As Gallian (2016) puts it, abstract algebra “provides a common language that connects diverse areas of mathematics, revealing profound insights that often go unnoticed in more specialised studies.”
Challenges and the Future
Despite its utility, abstract algebra remains underappreciated outside mathematical circles. Part of the issue is its steep learning curve and the abstract nature of its content. However, with the increasing importance of data security, artificial intelligence, and quantum technologies, the demand for individuals who understand these structures is growing.
New teaching strategies, such as interactive theorem proving, visual algebra software, and gamified algebraic puzzles, are helping to demystify the subject for learners. By making algebra tangible and explorative, educators hope to inspire a new generation to appreciate the beauty of structure and the logic of systems.
Abstract algebra stands as a testament to the power of human reasoning—a branch of mathematics that dares to question not just what equations can be solved, but what structures make those solutions possible. From the ancient study of numbers to the cryptographic protocols that protect our digital identities, abstract algebra continues to shape the mathematical, technological, and philosophical landscape of the modern world.
Understanding abstract algebra is more than a mathematical exercise; it is an invitation to see the hidden symmetries and deep logic that govern both nature and information. As our world becomes increasingly complex, the tools of abstract algebra offer a clarifying lens, revealing the elegant structures beneath apparent chaos.
References
Fraleigh, J. B. (2013). A First Course in Abstract Algebra (7th ed.). Pearson.
Gallian, J. A. (2016). Contemporary Abstract Algebra (9th ed.). Cengage Learning.
Hall, B. C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction (2nd ed.). Springer.
Huffman, W. C., & Pless, V. (2010). Fundamentals of Error-Correcting Codes. Cambridge University Press.
Mohanty, A. (2024). “Conceptual Scaffolding in Abstract Algebra: Cognitive Load and Pedagogical Strategies.” Journal of Mathematical Education, 28(1), 15–33.
Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information (10th Anniversary ed.). Cambridge University Press.
Stewart, I. (2004). Galois Theory (3rd ed.). Chapman and Hall/CRC.
Stinson, D. R., & Paterson, M. B. (2018). Cryptography: Theory and Practice (4th ed.). CRC Press.