Financial Management: Overview of Key Study Topics Within the Field
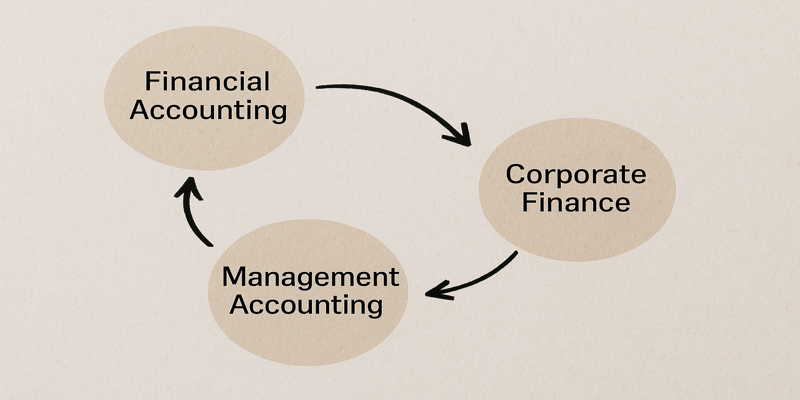
Financial Management plays a central role in the success and sustainability of modern organisations. It encompasses the planning, organisation, control, and monitoring of financial resources to achieve corporate objectives and maximise shareholder wealth. Within this broad discipline, three major areas are often studied in depth: Financial Accounting, Management Accounting, and Corporate Finance. Each area contributes uniquely to the field, shaping both internal decision-making and external reporting practices. 1.0 Financial Accounting Financial Accounting deals with the systematic recording, summarising, and reporting of an organisation’s financial transactions. It ensures that financial information is presented accurately in compliance with established standards such as International Financial Reporting Standards (IFRS) and Generally Accepted Accounting Principles (GAAP). According to Shah (2013), the primary purpose of financial accounting is to prepare financial statements, including the balance sheet, income statement, and cash flow statement, which communicate a company’s financial health to external stakeholders such as investors, regulators, and creditors. Transparency and accountability are essential, as inaccurate reporting can undermine investor confidence and lead to financial scandals, as seen in the cases of Enron and WorldCom (Bushman & Smith, 2001). Financial accounting also provides the foundation for corporate governance by ensuring reliable financial disclosures. Research by Sloan (2001) highlights the importance of accounting information in monitoring managerial performance and reducing information asymmetry between managers and shareholders. A practical example can be found in publicly listed companies on the London Stock Exchange, where adherence to IFRS ensures comparability and investor trust. Companies such as Barclays PLC or BP publish audited annual reports that serve not only as compliance documents but also as communication tools for investors and analysts. Thus, financial accounting underpins the credibility of financial markets by providing standardised information essential for investment and lending decisions. 2.0 Management Accounting While financial accounting primarily addresses external reporting, Management Accounting focuses on internal decision-making. It provides managers with timely, relevant, and forward-looking information to plan, control, and evaluate organisational activities. Vaivio (1999) emphasises that management accounting is not limited to financial measures but increasingly incorporates non-financial metrics, such as customer satisfaction, employee performance, and sustainability indicators. This shift reflects the evolving nature of competitive business environments where intangible assets play a critical role. Key techniques in management accounting include: Budgeting: Developing detailed financial plans for future operations. Cost analysis: Determining the cost structure of products and services to support pricing and profitability decisions. Variance analysis: Identifying differences between planned and actual performance. Financial forecasting: Predicting future financial outcomes to guide strategic choices. Banerjee (2012) notes that management accounting serves as the backbone of strategic planning by equipping managers with tools to evaluate scenarios, allocate resources, and optimise operations. For instance, companies like Unilever and Tesco use activity-based costing (ABC) to allocate overhead costs more accurately, thereby improving profitability analysis. Moreover, management accounting enhances performance evaluation. Techniques such as the Balanced Scorecard, introduced by Kaplan and Norton, integrate financial and non-financial measures to assess overall organisational effectiveness (Melicher & Norton, 2013). In essence, management accounting provides the decision-support framework required for businesses to adapt to changing environments and maintain competitiveness. 3.0 Corporate Finance Corporate Finance addresses the financial decisions that corporations must make to maximise shareholder value. It is concerned with three core areas: Investment decisions (capital budgeting) – determining which projects or assets to invest in. Financing decisions – choosing the optimal mix of debt and equity to fund operations. Dividend policy – deciding how much profit should be retained versus distributed to shareholders. As Brealey, Myers, and Allen (2014) outline in Principles of Corporate Finance, the overarching goal of corporate finance is value maximisation. This involves balancing risk and return when allocating resources. A key concept is capital structure. Theories such as the Modigliani-Miller theorem argue that, under perfect market conditions, the value of a firm is unaffected by its financing choices. However, in practice, factors like taxation, bankruptcy costs, and agency conflicts make financing decisions critical (Jensen & Smith, 2006). Corporate finance also covers mergers and acquisitions (M&A), where strategic decisions about combining or acquiring firms can reshape entire industries. For example, the Vodafone–Mannesmann merger in 2000, valued at over €180 billion, illustrates how corporate finance principles influence global business landscapes (Arnold & Lewis, 2019). Another crucial area is risk management. Companies employ financial derivatives such as futures, options, and swaps to hedge against risks associated with interest rates, foreign exchange, or commodity prices (Keown, 2004). Multinational firms like BP and Airbus regularly use such instruments to stabilise cash flows in volatile markets. Corporate finance extends beyond private firms. Government bodies also apply these principles when issuing bonds or financing infrastructure projects, highlighting its wide applicability across economic sectors. Financial Management integrates the disciplines of Financial Accounting, Management Accounting, and Corporate Finance to provide a comprehensive framework for managing financial resources effectively. Financial accounting ensures accountability and transparency for external stakeholders, while management accounting supports strategic decision-making and operational efficiency. Corporate finance, on the other hand, focuses on maximising shareholder value through informed investment, financing, and risk management strategies. Together, these fields form the bedrock of modern financial practice. Whether ensuring regulatory compliance, improving internal efficiency, or enhancing shareholder returns, financial management remains a critical discipline in both academic study and practical application. Its importance continues to grow in an increasingly globalised and competitive business environment, making it an indispensable area of knowledge for aspiring business leaders and finance professionals. References Arnold, G. & Lewis, D. (2019). Corporate Financial Management. 6th ed. Harlow: Pearson. [Available at: https://miemagazine.com/sample/Management/MG501-600/MG569/sample-Corporate%20Financial%20Management%206th%206E%20Glen%20Arnold.pdf] Banerjee, B. (2012). Financial Policy and Management Accounting. 2nd ed. New Delhi: PHI Learning. Brealey, R.A., Myers, S.C. & Allen, F. (2014). Principles of Corporate Finance. 11th ed. New York: McGraw-Hill. Bushman, R.M. & Smith, A.J. (2001). Financial accounting information and corporate governance. Journal of Accounting and Economics, 32(1–3), pp. 237–333. [https://papers.ssrn.com/sol3/Delivery.cfm?abstractid=253302] Jensen, M.C. & Smith, C.W. (2006). The Theory of Corporate Finance: A Historical Overview. New York: McGraw-Hill. Keown, A.J. (2004). Foundations of Finance: The Logic and Practice of Financial Management. 4th ed. New Jersey: Pearson. Melicher, R.W. & Norton, … Read more