Kinematics is one of the fundamental pillars of classical mechanics, focusing on the description of motion without considering the forces that cause it. Often regarded as the first stepping stone into the study of physics, kinematics equips learners and professionals with the tools to understand how objects move in space and time — a crucial foundation for everything from engineering design to space exploration.
In this article, we delve into the essence of kinematics, exploring its basic concepts, practical applications, historical development, and relevance in both education and technological advancement.
What Is Kinematics?
Derived from the Greek word kinēma, meaning “movement,” kinematics is the branch of mechanics that deals solely with the geometry of motion. Unlike dynamics, which examines the why of motion through forces, kinematics answers the how of motion by studying position, displacement, velocity, and acceleration over time (Serway & Jewett, 2018).
This branch is especially important in cases where understanding the trajectory or path of motion is necessary, without being concerned about the underlying forces.
Core Concepts in Kinematics
Kinematics primarily applies to point particles or rigid bodies and operates under several key parameters:
1.0 Displacement
Displacement is a vector quantity that represents the change in position of an object. Unlike distance, which is scalar and always positive, displacement includes both magnitude and direction (Knight, 2017).
2.0 Velocity
Velocity is defined as the rate of change of displacement with respect to time. An object moving in a straight line at constant speed has constant velocity. However, velocity can change with either magnitude or direction (Young & Freedman, 2019).
3.0 Acceleration
Acceleration is the rate at which velocity changes over time. It can be caused by a change in speed, direction, or both. Positive acceleration increases velocity, while negative acceleration (or deceleration) decreases it.
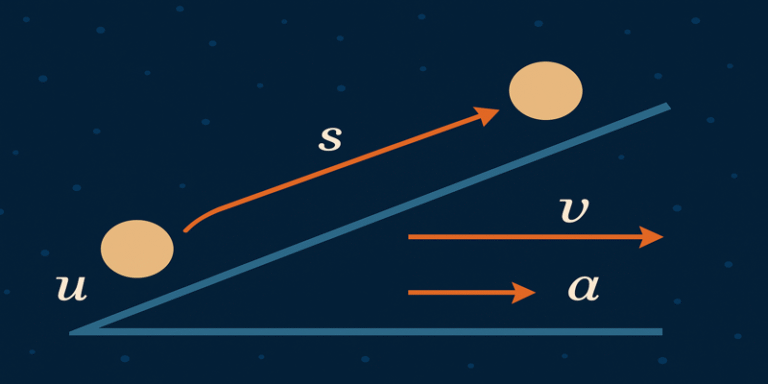
Equations of Motion
One of the most widely taught aspects of kinematics is the set of equations of uniformly accelerated motion. These equations assume constant acceleration and are indispensable in both theoretical physics and applied engineering problems:
- v=u+atv = u + atv=u+at
Final velocity = Initial velocity + (acceleration × time) - s=ut+12at2s = ut + \frac{1}{2}at^2s=ut+21at2
Displacement = (Initial velocity × time) + ½ (acceleration × time²) - v2=u2+2asv^2 = u^2 + 2asv2=u2+2as
Final velocity squared = Initial velocity squared + 2 × acceleration × displacement
These equations can be used to model falling objects, projectiles, or vehicles under uniform acceleration (Serway & Jewett, 2018).
Types of Motion in Kinematics
1.0 Linear Motion
Also known as rectilinear motion, this involves movement in a straight line. Examples include a car moving along a straight road or a skydiver falling directly downward.
2.0 Projectile Motion
Involves motion under the influence of gravity in two dimensions — typically horizontal and vertical. Common examples include the path of a ball thrown across a field or a missile following a curved trajectory (Halliday, Resnick & Walker, 2014).
3.0 Circular Motion
This involves movement along a circular path. It introduces angular variables like angular displacement, angular velocity, and centripetal acceleration. A satellite orbiting Earth or a car turning around a roundabout exhibits circular motion.
Real-World Applications of Kinematics
Despite its theoretical appearance, kinematics has profound implications across multiple domains:
1.0 Automotive Engineering
Engineers use kinematic equations to model braking systems, crash simulations, and vehicle dynamics. Understanding motion helps improve safety features, efficiency, and comfort.
2.0 Robotics and Automation
In robotics, kinematics is used to model and control motion in robotic arms and automated machinery. Precise positioning and speed control rely heavily on solving kinematic equations (Craig, 2005).
3.0 Biomechanics and Sports Science
Kinematic analysis is used to study gait, muscle movement, and joint motion in humans. It is vital for injury prevention, athletic training, and even designing prosthetic limbs (McGinnis, 2020).
4.0 Aerospace and Astronomy
In launching spacecraft, understanding how an object’s position and velocity change over time without external interference is essential. From satellites in orbit to re-entry calculations, kinematics is foundational (Smart & Green, 2013).
Educational Importance
Kinematics forms a major portion of high school and undergraduate physics curricula. It introduces students to the discipline’s problem-solving nature and develops essential analytical skills.
According to an article by Hake (1998), active engagement with kinematics through graphical methods, real-life examples, and computer simulations improves conceptual understanding and student retention.
Platforms like Khan Academy and PhET Interactive Simulations offer valuable interactive resources that visualise motion in ways textbooks cannot, enhancing comprehension for visual learners (PhET, 2023).
Historical Development of Kinematics
Though formalised in the 17th century, ideas related to motion trace back to Aristotle, who believed objects moved according to their nature. This view was challenged by Galileo Galilei, who laid the groundwork for kinematics by studying objects rolling down inclined planes and deducing that objects accelerate uniformly under gravity (Drake, 1999).
Galileo’s findings influenced Isaac Newton, whose Principia Mathematica synthesised the understanding of motion into a unified framework. While Newton focused on forces, Galileo’s approach to motion independent of force remains the foundation of kinematics today.
Modern Research and Technologies
Today, kinematics is being extended through motion capture, computer vision, and machine learning. These tools allow detailed analysis of motion in medicine, sports, and animation.
For example, in healthcare, gait analysis systems help diagnose neurological conditions through deviations in walking patterns. In the film industry, kinematics enables realistic animation, capturing subtle human movements for CGI characters.
Moreover, inverse kinematics — solving for the inputs needed to produce a desired output — is a crucial concept in fields such as virtual reality, game development, and robotic control systems (Spong et al., 2020).
In summary, kinematics is not just a basic topic confined to classroom problems; it is a core scientific tool that underpins our ability to describe and predict the behaviour of objects in motion. From the simplicity of a ball rolling down a hill to the complexity of satellite trajectories, the principles of kinematics allow us to make accurate, meaningful interpretations of the world around us.
As both a learning module and a research tool, kinematics continues to evolve, demonstrating its relevance across centuries and its utility across disciplines.
References
Craig, J.J. (2005) Introduction to Robotics: Mechanics and Control. 3rd ed. Upper Saddle River: Pearson.
Drake, S. (1999) Galileo: A Very Short Introduction. Oxford: Oxford University Press.
Halliday, D., Resnick, R., & Walker, J. (2014) Fundamentals of Physics. 10th ed. Hoboken: Wiley.
[Hake, R.R. (1998) ‘Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses’, American Journal of Physics, 66(1), pp.64–74. DOI: 10.1119/1.18809
Knight, R.D. (2017) Physics for Scientists and Engineers: A Strategic Approach with Modern Physics. 4th ed. Boston: Pearson.
McGinnis, P.M. (2020) Biomechanics of Sport and Exercise. 3rd ed. Champaign: Human Kinetics.
PhET Interactive Simulations. (2023) Motion in 2D Simulation. University of Colorado Boulder. Available at: https://phet.colorado.edu (Accessed: 7 August 2025).
Serway, R.A. & Jewett, J.W. (2018) Physics for Scientists and Engineers with Modern Physics. 10th ed. Boston: Cengage Learning.
Smart, W.M. & Green, R.M. (2013) Textbook on Spherical Astronomy. 6th ed. Cambridge: Cambridge University Press.
Spong, M.W., Hutchinson, S., & Vidyasagar, M. (2020) Robot Modeling and Control. 2nd ed. Hoboken: Wiley.
Young, H.D. & Freedman, R.A. (2019) University Physics with Modern Physics. 15th ed. Harlow: Pearson.