Newtonian mechanics, also known as classical mechanics, is one of the most important frameworks in the history of science. It provides a mathematical and conceptual structure for understanding the motion of bodies under the influence of forces. Rooted in the 17th-century insights of Sir Isaac Newton, this theory has shaped the development of physics, engineering, and astronomy for over three centuries.
While modern physics has introduced relativistic and quantum perspectives, Newtonian mechanics remains the bedrock for much of what we understand about everyday motion. It is essential in fields ranging from mechanical design and space travel to sports science and civil engineering.
1.0 The Birth of Newtonian Mechanics
The origins of Newtonian mechanics can be traced back to 1687, with the publication of Newton’s seminal work, Philosophiæ Naturalis Principia Mathematica, often simply referred to as the Principia (Newton, 1999 [1687]). In this work, Newton unified earlier concepts of motion and force, providing a systematic framework governed by three fundamental laws, now known as Newton’s laws of motion.
His ideas built upon earlier works by Galileo Galilei and Johannes Kepler, but Newton’s brilliance was in generalising and formalising them into universal laws that could predict the behaviour of objects from falling apples to planetary orbits (Westfall, 1983).
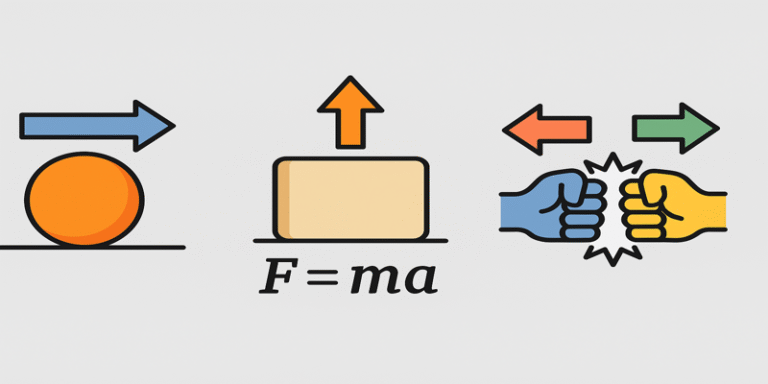
2.0 Newton’s Three Laws of Motion
2.1 First Law: The Law of Inertia
An object at rest remains at rest, and an object in motion continues in motion with constant velocity unless acted upon by a net external force.
This principle, known as inertia, describes the natural tendency of objects to resist changes in their state of motion. It explains why seatbelts are essential in vehicles — without them, passengers would continue moving forward during a sudden stop (Young & Freedman, 2019).
In engineering, this law is used to determine conditions under which systems remain static or continue moving uniformly. It underpins the concept of equilibrium in structures and machinery (Hibbeler, 2016).
2.2 Second Law: Force and Acceleration
The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
Mathematically expressed as F = ma, this law defines how forces cause changes in motion. It enables us to calculate the required force to move an object of known mass or determine how a known force will accelerate a given mass.
This law is essential in designing vehicles, aircraft, and even robotic systems. For example, the thrust force generated by an aircraft engine must be sufficient to accelerate the aircraft’s mass to lift-off speed (Meriam & Kraige, 2013).
2.3 Third Law: Action and Reaction
For every action, there is an equal and opposite reaction.
This law explains interactions between objects. When you push on a wall, it pushes back with equal force. This is why rockets can propel themselves in space — the expulsion of gas backward produces an equal force pushing the rocket forward (Giancoli, 2008).
Applications are found in propulsion systems, biomechanics (such as walking and running), and even in the analysis of structures under dynamic loading.
3.0 Real-World Applications of Newtonian Mechanics
3.1 Engineering and Construction
Newtonian mechanics governs the behaviour of structures, ensuring that bridges, towers, and buildings can withstand various forces, from gravity to wind loads. Engineers use statics and dynamics, both rooted in Newton’s laws, to calculate forces and design safe, efficient systems (Beer et al., 2015).
For instance, when designing a suspension bridge, engineers must balance gravitational forces and tension using Newton’s laws to ensure the bridge remains stable and doesn’t collapse under load.
3.2 Spaceflight and Orbital Mechanics
Modern space exploration still relies heavily on Newton’s principles. Calculations of rocket trajectories, satellite orbits, and interplanetary travel are grounded in Newtonian gravity and the laws of motion. Kepler’s laws of planetary motion, which describe elliptical orbits, are derived from Newton’s formulation of gravity (Khan et al., 2020).
Although general relativity refines Newton’s gravity for extreme cases, Newtonian mechanics is more than sufficient for most space missions and remains computationally efficient.
4.1 Biomechanics and Sports Science
In analysing human motion, Newton’s laws explain how muscles produce force and how body segments accelerate. From sprinting to swimming, every motion is a demonstration of these principles. Sports scientists use Newtonian models to improve athletic performance, reduce injury, and optimise training (Bartlett, 2007).
5.0 Limitations of Newtonian Mechanics
While extraordinarily powerful, Newtonian mechanics is not without limits. It assumes:
- Time and space are absolute.
- Forces act instantaneously.
- Mass is constant.
These assumptions break down under certain conditions. For example:
- At speeds approaching the speed of light, special relativity takes over (Einstein, 1905).
- At atomic scales, quantum mechanics governs interactions.
Nonetheless, within its valid range—low speeds and macroscopic scales—Newtonian mechanics remains accurate and indispensable.
6.0 Educational Importance
Newtonian mechanics is the first formal system of physics taught in schools and universities. It introduces students to the power of mathematical modelling, problem-solving, and empirical reasoning.
Using free-body diagrams, vector analysis, and equation solving, students learn to analyse physical systems and predict outcomes. This not only builds foundational understanding for further study in physics and engineering but also fosters critical thinking and analytical skills (Knight, 2016).
7.0 Influence on Scientific Thought
Beyond physics, Newton’s ideas influenced the Enlightenment, shaping how thinkers approached problems. His concept of a universe governed by predictable laws laid the groundwork for the scientific method.
Newtonian mechanics has also inspired mathematical advances, including differential equations, vector calculus, and linear algebra—tools that are now ubiquitous across all sciences and engineering disciplines.
Newtonian mechanics is much more than a set of three equations. It is a comprehensive framework that continues to explain and predict much of the physical world around us. From launching rockets to building bridges, from analysing sports motion to simulating mechanical systems, Newton’s insights remain profoundly relevant.
Though later superseded in some domains by relativity and quantum theory, Newtonian mechanics remains the cornerstone of classical physics. Its elegance, simplicity, and predictive power ensure its continued use in science, education, and engineering.
References
Bartlett, R. (2007) Introduction to Sports Biomechanics: Analysing Human Movement Patterns. 2nd ed. London: Routledge.
Beer, F.P., Johnston, E.R., Mazurek, D.F. and Eisenberg, E.R. (2015) Vector Mechanics for Engineers: Statics and Dynamics. 11th ed. New York: McGraw-Hill.
Einstein, A. (1905) Zur Elektrodynamik bewegter Körper. Annalen der Physik, 17(10), pp.891–921.
Giancoli, D.C. (2008) Physics: Principles with Applications. 6th ed. Pearson Education.
Hibbeler, R.C. (2016) Engineering Mechanics: Dynamics. 14th ed. Pearson.
Khan, M. I., Khan, M. A., & Butt, M. F. (2020) ‘Applications of Newtonian Mechanics in Modern Space Programs’, Journal of Space Technology, 10(2), pp. 45–54.
Knight, R.D. (2016) Physics for Scientists and Engineers: A Strategic Approach. 4th ed. Pearson.
Meriam, J.L. & Kraige, L.G. (2013) Engineering Mechanics: Dynamics. 7th ed. Wiley.
Newton, I. (1999 [1687]) The Principia: Mathematical Principles of Natural Philosophy, trans. Cohen, I.B. & Whitman, A. Berkeley: University of California Press.
Westfall, R.S. (1983) Never at Rest: A Biography of Isaac Newton. Cambridge: Cambridge University Press.
Young, H.D. & Freedman, R.A. (2019) University Physics with Modern Physics. 15th ed. Pearson.